Object Tracking With Spiking Neural Networks

Last semester, I had the fortune of doing some work with the Human Brain Project, an EU-funded research project with the aim of understanding, mapping and partly reconstructing the human brain through computer simulations and actual hardware. Using the Neurorobotics Platform (NRP), an environment for developing and running experiments with spiking neural networks and simulated robots, I implemented a closed loop control-based solution for tracking an object in space using spiking neural networks. In this post, I am outlining spiking neural networks, the Neurorobotics platform and how one can implement simple control loops for solving tracking tasks using spiking neural networks and the NRP toolset. The code for the corresponding NRP experiment can be found on GitHub.

Spiking Neural Networks

Spiking neural networks attempt to model the neurons of the human brain much more closely than the “classical” neural networks used for deep learning. While in deep neural networks, units instantly react to their inputs and produce outputs immediately, spiking neural networks are dynamical systems: The output at any given time is dependent on previous inputs as well as on the state of the neuron at that time. The physiology of biological neurons and the relevance of dynamical systems in the modelling of neurons is explained in some detail in Jack Terwilliger’s blog post.

Neuron Models

Many different neuron models exist and spiking neural networks often combine multiple models. In all models, neurons fire impulses (or spikes) dependent on the current and past input voltage. The input voltage is computed based on the spike activity of other, connected neurons. The most simple “integrate-and-fire” model integrates over the input voltage, emits a spike when the integrated input reaches a threshold and resets the integrator to zero. Most commonly, the integrator is leaky: Its value decreases over time. Mathematically, a leaky integrator can be modelled using a simple linear differential equation and is functionally equivalent to an RC circuit. Much more complex models have been devised in literature to add a refractory period, during which the neuron cannot fire, or the capacity to oscillate or resonate. While these models model the behavior of human neurons much more closely, simple models such as integrate-and-fire incur less computational overhead and often suffice to solve real-world problems with spiking neural networks.

Computing with Spiking Neural Networks

It has been shown that every possible function can be realized with a traditional deep neural network. Simples spiking neural networks work similarly to traditional deep neural networks: The network is specified by connecting input populations of neurons to output populations using synapses. Arbitrarily many layers can be formed. In its simplest form, a synapse connects M input neurons to N output neurons. With the simplest possible synapse, the strength of each connection is specified by a multiplier, the synapse weight, resulting in an NxM weight matrix for a fully connected synapse which encodes for each output neuron which input neuron contributes how much to its input voltage. In other words, each output neuron’s input voltage is the weighted sum of its inputs - just like in “regular” deep neural networks. More complex synapse models differ from the connections in traditional neural networks in that they model synapses in the human brain more closely, can be stateful and “learn” by changing their characteristics depending on the input spike frequency and timing, a property called spike-timing dependent plasticity. Learning with spiking neural networks still presents a number of open problems and constitutes a highly productive field of research.

Spiking neural networks mostly differ from deep neural networks because they are dynamical systems - their outputs depend on the inputs over time. Unlike deep neural networks, where information is encoded in tensors, spiking neural networks encode information in the spike train, the function of spiking activity over time, through the frequency and timing of spikes. Depending on the neuron model, spike emission may be stochastic; in this case, the information encoding is called a spike density code.

The Neurorobotics Platform

The Neurorobotics Platform (NRP) is an application developed by the Neurorobotics group of the Human Brain Project for developing and running experiments about controlling robots using spiking neural networks. Its backend is a combination of ROS for infrastructure and interaction with (simulated) robots, the Gazebo robot simulator and the NEST neural network simulator; it has a Javascript-based web interface and allows manipulation of the 3D environment, neural network and experiment setup in a browser. An NRP experiment is defined in an XML file and consists of a state machine, a brain file, an (SDF) environment model and an optional ROS launch file.

State Machine

The state machine defines any action on the part of the environment. If something in the environment needs to be moved, such as the target object for object tracking, or if objects need to be spawned at runtime, it can be done in a Python smach state machine. It has access to the environment, additionally loaded 3D models as well as to all available ROS topics and services.

Brain Definition and Transfer Functions

In the NRP, the brain consists of two components: A PyNN brain description file and one or more transfer functions. PyNN provides a simulator-independent interface to neural network simulators such as NEST. In the brain file, populations of spiking neurons are defined and connected through synapses. An example brain file for object tracking is provided below. Transfer functions map neuron activity to robot motion or vice versa - they are Python functions which are called in every cycle of the NRP’s Closed Loop Engine, and have access to both the brain as defined in the brain file and the ROS topics for robot control. In their purest form, transfer functions implement visuomotor coupling - a closed loop between neural activity and the resulting motion. This closed loop is crucial for implementing object tracking in the NRP.

Closed-Loop Control for Object Tracking

There are many approaches for tracking objects, many of which rely on direct or indirect solutions to the correspondence problem or particle filters. When humans track objects, however, they do not analytically compute two-dimensional convolutions with a reference pattern, like many traditional filter-based approaches do. Instead, humans move their eyes to keep the object in the center of their field of vision. When trying to evict a fly from your living room, for example, you constantly keep your eyes centered on the fly and follow its motion. This can be modelled in a straightforward way with a closed-loop control circuit: The sensors on the retina cause excitations of the neurons of the visual cortex; these excitation patterns instruct the eye and neck muscles to move in order to keep the tracked object in the center. Small deviations in the position of the tracked object cause compensatory movements of the eyes, which in turn cause the image on the retina to change, etc. In control theory terms, the retina is the sensor, the eye muscles are the controller and the position and orientation of the eyes are the controlled system.

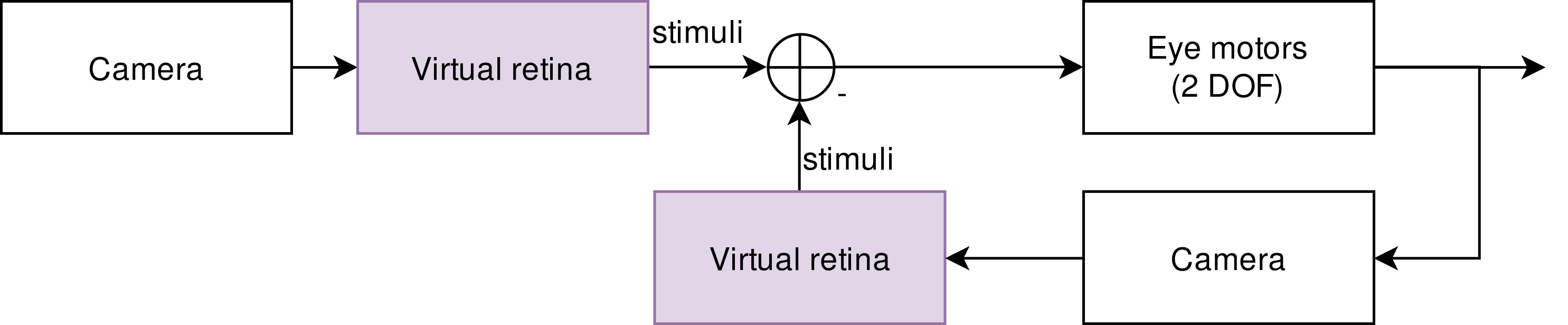
Because the NRP comes with a Closed Loop Engine (CLE), implementing closed loop control with spiking neural networks is relatively straightforward in the NRP. The spiking activity of an input population (“virtual retina”) encodes where in the field of vision a tracked object is located at a given time. Via a set of synapses and transfer functions (in the human brain, this would happen in the visual cortex and sensorimotor circuits), the outputs of this population are connected to the inputs of a motor population which, in turn, controls the joint actuators in the eye and neck of the robot.

Thimblerigger Experiment

To try this out, my colleagues and I created an experiment (the code is on GitHub) in which a simulated iCub robot is to play the thimblerigger game: A ball is hidden under one of three cups; after the cups are shuffled, the robot has to guess which cup the ball is hidden under. Humans instinctively approach this task by trying to follow the cup hiding the ball with their eyes. While it would be easier and probably more robust to solve this problem using traditional image processing and frame-by-frame analysis, we chose to implement a closed-loop solution for tracking which is as close to the human approach as possible to demonstrate how closed-loop control for visuomotor coupling can be implemented with spiking neural networks in just a few lines of code.

The experiment itself is defined using an SMACH state machine (the code for it is on GitHub). When the user starts the experiment, three red cups are spawned. One cup is selected at random to conceal a green ball. This cup is lifted to briefly reveal the ball, then lowered again. The cups are shuffled by moving them to a series of random permutations. In the end, the ball is revealed again - if the tracking system worked, the robot is now looking directly at the ball.

Virtual Retina & Brain File

The central component of our implementation is the brain file. The brain itself consists of two populations: An input population, representing the virtual retina, and an output population whose outputs are used to control the robot’s joints.

from hbp_nrp_cle.brainsim import simulator as sim
import numpy as np

resolution = 17
n_motors = 4  # down, up, left, right

sensors = sim.Population(resolution * resolution, cellclass=sim.IF_curr_exp())
down, up, left, right = [sim.Population(1, cellclass=sim.IF_curr_exp()) for _ in range(n_motors)]

indices = np.arange(resolution * resolution).reshape((resolution, resolution))
ones = np.ones(shape=((resolution // 2) * resolution,1))

upper_half = sim.PopulationView(sensors, indices[:resolution // 2].flatten())
lower_half = sim.PopulationView(sensors, indices[resolution - resolution//2:].flatten())
left_half = sim.PopulationView(sensors, indices[:, :resolution // 2].flatten())
right_half = sim.PopulationView(sensors, indices[:, resolution - resolution//2:].flatten())

pro_down = sim.Projection(lower_half, down, sim.AllToAllConnector(), sim.StaticSynapse(weight=ones))
pro_up = sim.Projection(upper_half, up, sim.AllToAllConnector(), sim.StaticSynapse(weight=ones))
pro_left = sim.Projection(left_half, left, sim.AllToAllConnector(), sim.StaticSynapse(weight=ones))
pro_right = sim.Projection(right_half, right, sim.AllToAllConnector(), sim.StaticSynapse(weight=ones))

circuit = sensors + down + up + left + right

The sensors population contains the sensor neurons whose spike train correlates with the position of the tracked object. Each neuron is responsible for a small rectangular part of the field of view and spikes when a part of the tracked object is inside this rectangle. For our retina, we chose a resolution of 17x17 neurons, so sensors is a population of 289 neurons.

The down, up, left and right populations consist of one neuron each. They are our output or motor populations and encode whether and how quickly the eye is to move in either direction. For simplicity and mechanical stability,¹ we chose to actuate only iCub’s left eye as opposed to both eyes and used only the image from the left eye’s camera as opposed the combined (stereo) image.

upper_half, lower_half, left_half and right_half are PopulationViews which divide the sensors population into four different groups corresponding to larger regions in the image. Our down, up, left and right populations will end up controlling the eye, but we still need to somehow connect “what the retina sees” to these output populations. To that end, we divide the retina into these upper, lower, left and right areas. If the tracked object is in the upper half, the neurons in the upper_half PopulationView fire more frequently than those in the other areas, so we know that we have to move our eye upwards to keep the tracked object in the center of the field of view.

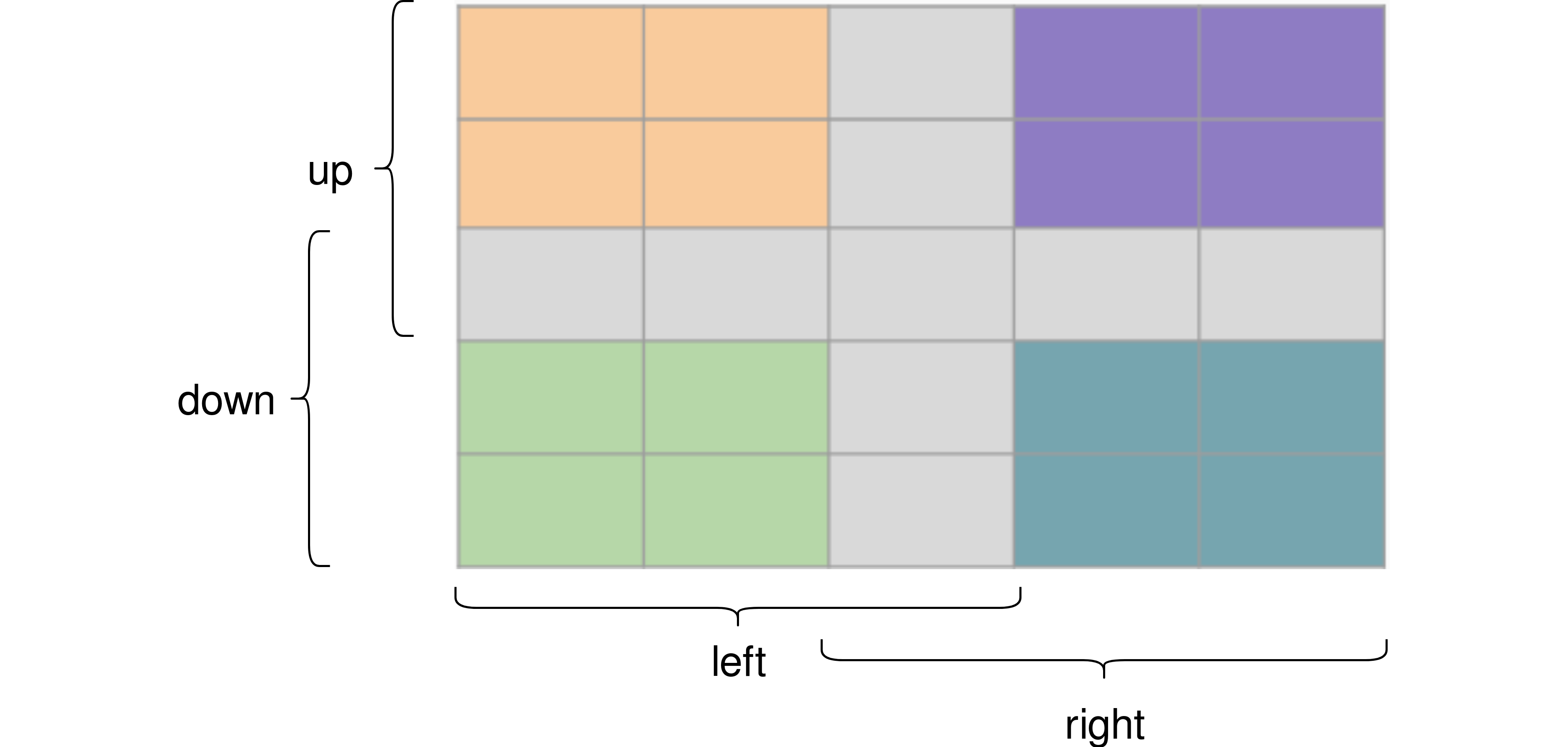
The coupling between the output of the retinal sensors and the down, up, left and right motor populations is done via the Projections pro_down, pro_up, pro_left and pro_right. Projections are connections between populations (or, in our case, PopulationViews) which define which neurons from the input population are connected to which neurons from the output population (fully connected (all to all) in our case) as well as the synapse type used for the connections. We use StaticSynapses whose properties do not change over time. The weight parameter is a matrix defining the connection weights. Because we used an AllToAllConnector, weight is a 136 * 1 matrix assigning a weight for each of the incoming connections from the (17//2)*17 input neurons per half of the retina. Our weight matrix contains only ones - each input neuron is weighted equally for the computation of the output. How the input spike trains are aggregated in each motor neuron and what their output looks like is defined by the cellclass used when defining the motor neuron populations. We use PyNN’s IF_curr_exp, a basic integrate-and-fire model.

Transfer Functions

In the NRP, transfer functions connect the brain defined in the brain file to the robot and the environment. Activating sensor populations based on input from (simulated) sensors such as the cameras in iCub’s eyes or from joint encoders as well as the coupling between the outputs of the motor neurons and the joint actuators is done in transfer functions. To implement our object-tracking solution, we need two transfer functions: One to connect the sensory input (the camera image) to the sensor population, and another to connect the motor neurons to the eye’s actuators.

Object detection

# detect_object.py

import numpy as np
import sensor_msgs.msg
import std_msgs.msg
from cv_bridge import CvBridge
@nrp.MapRobotSubscriber("camera", Topic("/icub_model/left_eye_camera/image_raw", sensor_msgs.msg.Image))
@nrp.MapRobotSubscriber("shuffle_status_sub", Topic("/group_3/shuffling", std_msgs.msg.Bool))
@nrp.MapSpikeSource("sensors", nrp.map_neurons(range(0, nrp.config.brain_root.resolution ** 2), lambda i: nrp.brain.sensors[i]), nrp.dc_source)
@nrp.Robot2Neuron()
def grab_image(t, camera, shuffle_status_sub, sensors):
    resolution = nrp.config.brain_root.resolution

    # Take the image from the robot's left eye
    image_msg = camera.value
    if image_msg is not None:
        cvBridge = CvBridge()

        img = cvBridge.imgmsg_to_cv2(image_msg, "rgb8")
        img_height, img_width, color_dim = img.shape

        detect_red = shuffle_status_sub.value.data if shuffle_status_sub.value is not None else False

        if not detect_red:
            # Detect green in the whole image
            col_width = img_width // resolution
            row_height = img_height // resolution
            green_threshold = 0.5
            amp_scaling_factor = 32.
            
            # Split the image into regions of same size
            # Sensor neurons are addressed in row_major order, top left to bottom right
            # Loop over the neurons in the retina...
            for row_idx in range(resolution):
                for col_idx in range(resolution):
                    x_start = col_idx * col_width
                    x_end = x_start + col_width
                    y_start = row_idx * row_height
                    y_end = y_start + row_height
                    mean_red = np.mean(img[y_start:y_end,x_start:x_end,0])
                    mean_green = np.mean(img[y_start:y_end,x_start:x_end,1])
                    mean_blue = np.mean(img[y_start:y_end,x_start:x_end,2])

                    green_proportion = mean_green / float(mean_red + mean_green + mean_blue)

                    idx = row_idx * resolution + col_idx
                    amp = amp_scaling_factor * green_proportion if green_proportion > green_threshold else 0

                    sensors[idx].amplitude = amp
        else:
          # Detect red in the center of the image
          # ...

detect_object.py is a Robot2Neuron transfer function, meaning that information is sent from the robot (or the environment) to the brain. The inputs of the transfer function are defined using the NRP’s decorator syntax and consist of a subscriber to the camera’s ROS topic, the sensor population and a subscriber to the topic published by the experiment state machine which announces the current state of the experiment (true if shuffling, false otherwise). This is required because during shuffling, the object to be tracked is the red cup concealing the ball, while during the reveal in the beginning, the green ball must be tracked.

In the central loop, we iterate over all neurons in the retina, compute this neuron’s rectangular area of the field of view and compute the mean for each RGB channel over this region. The neuron’s amplitude (proportional to its firing rate) is set in proportion to the “amount” of green in the region relative to the other primary colors. This has the effect that neurons which “see” green fire more frequently than others. Because the sensor neurons are iterated using a nested loop, like for a 2D array, the sensor neuron activity spatially encodes the positions of green things in the image - and because of the wiring defined in the brain, the down, up, left and right motor populations are excited according to these positions: left fires frequently if there is a lot of green in the left side of the image, etc.

The code for tracking red objects has been omitted for brevity but works similarly with the only exception that not the entire image is considered, but a rectangular area around the center of the image, causing the margins to be ignored. This is necessary because three cups may be in the image at any given time, but we only want to track the one we centered on when the green ball was revealed.

Object following

The last remaining component of our solution is the transfer function for following the moving object (depending on the stage of the experiment either the ball or the cup) with iCub’s left eye. To that end, the outputs of the down,up, left and right motor populations must be connected to the two actuators for moving the eye.

# follow_object.py

import numpy as np
@nrp.MapSpikeSink("motors_down", nrp.brain.down, nrp.leaky_integrator_alpha)
@nrp.MapSpikeSink("motors_left", nrp.brain.left, nrp.leaky_integrator_alpha)
@nrp.MapSpikeSink("motors_up", nrp.brain.up, nrp.leaky_integrator_alpha)
@nrp.MapSpikeSink("motors_right", nrp.brain.right, nrp.leaky_integrator_alpha)
@nrp.MapRobotPublisher('eye_tilt_pos', Topic('/robot/eye_tilt/pos', std_msgs.msg.Float64))
@nrp.MapRobotPublisher('eye_pan_pos', Topic('/robot/left_eye_pan/pos', std_msgs.msg.Float64))
@nrp.MapRobotPublisher('eye_tilt_vel', Topic('/robot/eye_tilt/vel', std_msgs.msg.Float64))
@nrp.MapRobotPublisher('eye_pan_vel', Topic('/robot/left_eye_pan/vel', std_msgs.msg.Float64))
@nrp.MapRobotSubscriber("joint_state_sub", Topic("/robot/joints", sensor_msgs.msg.JointState))
@nrp.MapRobotSubscriber("shuffle_status_sub", Topic("/group_3/shuffling", std_msgs.msg.Bool))
@nrp.Neuron2Robot()
def center_on_green(t, motors_down, motors_left, motors_up, motors_right, eye_tilt_pos, eye_pan_pos, eye_tilt_vel, eye_pan_vel, joint_state_sub, shuffle_status_sub):

    stage_two = shuffle_status_sub.value.data if shuffle_status_sub.value is not None else False

    if not stage_two:
        # Stage one: Velocity-controlled motion to green ball
        scaling_factor = 3
        tilt = scaling_factor * (motors_up.voltage - motors_down.voltage)
        pan = scaling_factor * ( motors_left.voltage - motors_right.voltage)
        eye_tilt_vel.send_message(std_msgs.msg.Float64(tilt))
        eye_pan_vel.send_message(std_msgs.msg.Float64(pan))

    else:
        # Stage two: Position-controlled motion to red cup
        scaling_factor = 0.03
        joint_names = joint_state_sub.value.name
        joint_positions = joint_state_sub.value.position
        current_tilt = joint_positions[joint_names.index("eye_tilt")]
        current_pan = joint_positions[joint_names.index("left_eye_pan")]

        tilt = current_tilt + scaling_factor * (motors_up_stage_two.voltage - motors_down_stage_two.voltage)
        pan = current_pan + scaling_factor * ( motors_left_stage_two.voltage - motors_right_stage_two.voltage)

        eye_tilt_pos.send_message(std_msgs.msg.Float64(tilt))
        eye_pan_pos.send_message(std_msgs.msg.Float64(pan))

follow_object.py is a Neuron2Robot transfer function for mapping brain activity to robot motion. eye_tilt_pos, eye_pan_pos, eye_tilt_vel and eye_pan_vel are handles to the ROS topics for writing to the simulated robot’s velocity and position controllers for the left eye’s tilt and pan joints. In the first stage of the experiment, when centering on the green ball, we use the difference between up and downor left and right as inputs for the velocity controllers of the corresponding joints. We chose to use the velocity controllers for smoother control, as writing directly to the position controllers can cause very quick and jerky motion.

In the second stage of the experiment, when tracking a fast-moving red cup, we write directly to the position controllers, mainly for speed and for avoiding the oscillations which can occur when the input to a velocity controllers changes quickly.

Results

The resulting control scheme turned out to be surprisingly stable with hardly any oscillations. Because the voltages used for writing to the robot controllers are computed by integrating over the spike train, noise is reliably smoothed out and erratic motions are avoided. Only when the cups are shuffled extremely quickly is the controller too slow to follow. Our approach shows that spiking neural networks are well suited for the implementation of closed control loops, particularly when coupling sensor input with motion, and illustrates how architectural features of the NRP such as the closed loop engine can be leveraged to concisely implement object tracking using closed-loop control.